DIFFÉRENTIELLES (ÉQUATIONS)

DIFFÉRENTIELLES (ÉQUATIONS)

Les équations différentielles sont apparues historiquement tout au début du développement de l’analyse, en général à l’occasion de problèmes de mécanique ou de géométrie. Si, dans les premières investigations, l’on s’attachait surtout à en calculer les solutions au moyen de fonctions déjà connues, très vite ce point de vue s’affirma trop étroit; c’est qu’en effet le problème fondamental de la théorie des équations différentielles est de déduire les propriétés des solutions d’une équation ou d’un système donné de la forme analytique de ceux-ci; or, en général, les équations qui résultent d’une investigation théorique en mathématiques ou en physique ne sont pas explicitement intégrables et constituent, bien souvent, la principale source pour la définition de nouvelles fonctions dont les propriétés peuvent être prévues par une analyse systématique de grandes classes d’équations ou de systèmes.

On développera, dans les quelques rubriques qui suivent, les méthodes propres à mettre en évidence l’existence de solutions sous des conditions appropriées et à en étudier les propriétés les plus fondamentales.

1. Les sytèmes différentiels linéaires dans le champ réel

On se propose d’étudier l’existence et les propriétés des solutions du système différentiel linéaire:

pour i , j = 1, 2, ..., n , où les fonctions a ^ij (t ), b ⁱ (t ) de la variable réelle t sont à valeurs réelles ou complexes. Introduisant la matrice n 憐 n , c’est-à-dire à n lignes et à n colonnes, A(t ) = (a ^ij (t )), et les vecteurs x = (x ¹, x ², ..., x ⁿ ), b = (b ¹, b ², ..., b ⁿ ), on peut écrire au lieu de (1):

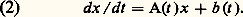On notera que toute équation différentielle linéaire d’ordre n :

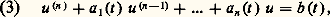u ^(j) désignant la dérivée d’ordre j de la fonction u (t ) peut être ramenée à la forme (1) ou (2) au moyen de substitutions x ¹ = u , x ² = u , ..., x ⁿ = u ^(n-1 , la matrice A et le vecteur b étant alors définis par:

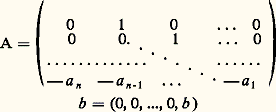Existence des solutions

Un premier résultat fondamental est donné par le théorème suivant: Le système

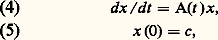où A(t ) est une matrice n 憐 n fonction continue de t 捻 [0, t ⁰] et où c est un vecteur donné, a une solution unique x (t ) définie pour t 捻 [0, t ⁰].

Il faut souligner qu’à l’équation (4) on a adjoint la condition initiale (5); on obtient ainsi un résultat d’existence et d’unicité.

On notera qu’au système (4), (5) on peut substituer l’équation intégrale équivalente:

qui se prête fort bien au calcul d’approximations successives inventé par Picard:

avec x ⁰ = c (cf. espaces MÉTRIQUES, chap. 7).

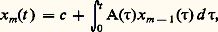On établit la convergence de la suite x ^m (t ) vers une fonction x (t ); on montre ensuite que x (t ) est solution de (4), (5) et qu’il y a unicité.

Le même type d’argument permet d’établir le théorème suivant: Le système

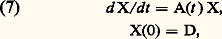où A(t ) est une matrice n 憐 n fonction continue de t 捻 [0, t ⁰], et D une matrice n 憐 n constante donnée, a une solution, matrice n 憐 n , X(t ), unique pour t 捻 [0, t ⁰].

On réservera, dans la suite, la notation X(t ) à cette solution quand on prend pour D la matrice identité I, et l’on dira que X(t ) est la matrice résolvante. Le théorème de Jacobi montre que:

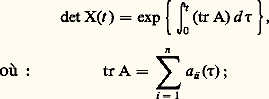ainsi la matrice X(t ) est toujours inversible.

Il est clair que la solution du système (4), (5) peut être représentée par x (t ) = X(t )c .

En prenant pour c les éléments de la base de l’espace vectoriel Rⁿ ou Cⁿ , on obtient n solutions de (4), qui sont les vecteurs dont les composantes sont inscrites successivement dans les colonnes de X(t ). Puisque det X(t ) 0, les vecteurs sont indépendants quel que soit t . D’ailleurs, si l’on dispose de n solutions indépendantes à l’instant t = 0, elles le demeurent pour tout t : on dira que c’est un système fondamental de solutions. Enfin, il ne peut exister plus de n solutions indépendantes.

Dans le cas de l’équation différentielle (3), supposée homogène (b (t ) = 0), les n solutions u ¹, u ², ..., u ⁿ sont indépendantes si, et seulement si, le déterminant de Wronski :

est 0 pour tout t . Il suffit que cela soit vrai pour une valeur particulière de t .

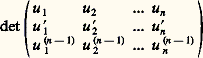L’équation linéaire non homogène

L’équation linéaire non homogène est l’équation:

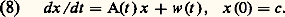Toute solution de (8) où A(t ) et w (t ) sont respectivement une matrice n 憐 n et un vecteur fonction continue donnée de t 捻 [0, t ⁰] et c un vecteur constant peut être recherchée sous la forme: x = X(t ) y , où X(t ) est la matrice résolvante de (7).

Il est aisé de voir que (8) conduit à:

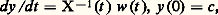système qui a la solution unique:

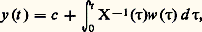d’où, pour (8), la solution unique:

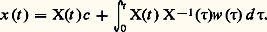Le cas des systèmes à coefficients constants

Si A est une matrice à éléments indépendants de t , la matrice résolvante X(t ) peut être représentée par la série convergente: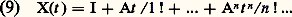

On pourra introduire sur l’espace vectoriel des matrices carrées n 憐 n la norme définie par:

avec la topologie correspondante, on peut s’assurer que la série (9) converge uniformément par rapport à t sur tout intervalle fini, et satisfait (7). Par le théorème d’unicité on montre aisément que: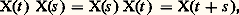

ce qui, avec (9), suggère la définition:

Il est connu que les puissances entières successives d’une matrice ne sont pas indépendantes; si f () est le polynôme caractéristique f () = det (A 漣I), on a f (A) = 0. Cela suggère que l’on peut donner à X(t ) une structure plus simple.

Pour tout nombre complexe, il existe un entier 益, le plus petit entier 閭 0 tel que: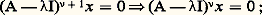

益 = 0 si, et seulement si, n’est pas valeur propre de la matrice A. Si est valeur propre, 益 est au plus égale à l’ordre de multiplicité algébrique de. Soit¹, ...,^k , avec k 諒 n , les valeurs propres distinctes de A, et soit:

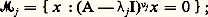les sous-espaces 紐^j sont sans élément commun autre que 0 et leur somme directe est Cⁿ ; on introduit les opérateurs de projection E^j par la formule E^jx = x ^j , où x = x ¹ + x ² + ... + x ^k , x ^j 捻 紐^j (décomposition spectrale). On établit que ces opérateurs permuttent avec A et que:

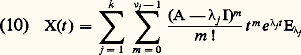est la matrice résolvante de (7).

Cette formule fondamentale montre que les éléments de la matrice X(t ) sont des sommes de produits d’exponentielle e size=1^{凞j t} par un polynôme en t dont le degré est inférieur à l’indice 益^j de^j , donc a fortiori à l’ordre de multiplicité algébrique de^j . On voit que les solutions de d X/dt = Ax convergent toutes vers 0 quand t+ 秊 si et seulement si les valeurs propres de la matrice A ont toutes leur partie réelle négative.

Le cas des systèmes à coefficients périodiques. La théorie de Floquet

Si X(t ) est la matrice résolvante de:

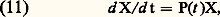où P(t ) est une matrice n 憐 n continue et périodique de période T par rapport à t , X(t + T) vérifie (11) et en vertu du théorème d’unicité: X(t + T) = X(t ) X(T). Comme X(T) est non singulière, il existe une matrice constante B telle que X(T) = e ^BT. La matrice Q(t ) = X(t )e ^-Bt est périodique de période T et on obtient la représentation: X(t ) = Q(t )e ^-Bt . Les valeurs propres de la matrice B sont les coefficients caractéristiques de la matrice périodique P(t ); il faut et il suffit qu’ils soient tous à partie réelle négative pour que toute solution de dx /dt = P(t )x tende vers 0 quand t+ 秊.

Stabilité des solutions

Revenons au cas général dx /dt = A(t )x , où A(t ) est une matrice fonction continue de t 捻 [0, + 秊]; il est souvent utile de connaître certaines propriétés asymptotiques de la solution, par exemple, de savoir si elles demeurent bornées ou tendent vers 0 quand t+ 秊. Pour conduire cette étude on utilise en général des méthodes de comparaison et, à cette fin, on peut introduire un concept de stabilité du genre suivant: les solutions de dx /dt = A(t )x seront dites stables par rapport à une propriété 戮 et une classe 杻 de matrices B(t ) si les solutions de dx /dt = (A(t ) + B(t ))x ont toutes les propriétés 戮 quel que soit B(t ) 捻 杻. On peut illustrer ce concept en citant le théorème suivant: Si les solutions dx /dt = Ax , où A est une matrice constante, sont bornées ou tendent vers 0 quand t+ 秊, alors il en est de même des solutions de:

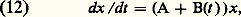pourvu que:

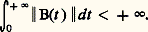Si toutes les solutions de dx /dt = Ax tendent vers 0 quand t+ 秊, il en sera de même des solutions de (12) pourvu que 瑩B(t ) 瑩 諒 k pour t assez grand, k étant un nombre qui ne dépend que de A.

2. Les systèmes différentiels linéaires dans le champ complexe

On peut reprendre les problèmes discutés précédemment en supposant que les fonctions qui interviennent dans la définition du système (1) ou (2) sont des fonctions analytiques de la variable z dans un domaine 行. On suppose d’abord que 行 est un domaine simplement connexe, c’est-à-dire un ensemble de points du plan complexe ouvert et connexe dont le complément par rapport au plan complexe muni du point à l’infini est connexe. On se propose de discuter le problème aux limites:

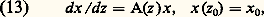avec z ⁰ 捻 行 donné, x ⁰ vecteur de Cⁿ donné, A(z ) matrice n 憐 n dont les éléments sont fonction holomorphe de z dans 行.

On peut établir, en se servant de la méthode d’approximations successives, que le système (13) a une solution unique x (z ) holomorphe dans 行. On peut aussi considérer le même problème pour le système matriciel:

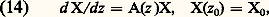X⁰ étant une matrice n 憐 n donnée, et on parvient à une conclusion analogue, c’est-à-dire existence d’une solution unique X(z ) matrice n 憐 n fonction holomorphe dans z dans 行.

Le théorème de Jacobi sous la forme:

et les considérations antérieures sur les systèmes de solutions indépendantes développées dans le cas de variable réelle demeurent valables ici.

La structure des solutions dans le voisinage d’un point singulier

Une situation nouvelle apparaît si l’on suppose que la matrice A(z ) possède des singularités ; plus précisément nous supposons que la singularité est en z = 0 et que A(z ) est holomorphe dans le voisinage 0 麗 |z | 麗 R; on précisera plus loin la nature de cette singularité ce peut être un pôle (ce qui signifie que les éléments a ^ij (z ) de A(z ) ont tous au plus une singularité polaire en z = 0) ou une singularité essentielle (ce qui signifie que, parmi les éléments a ^ij (z ), il en est un au moins qui possède, en z = 0, une singularité de cette nature).

D’après le résultat qui précède, on peut définir une solution de (14), X(z ) matrice non singulière (on suppose det X⁰ 0), fonction holomorphe de z dans tout domaine simplement connexe où A(z ) est holomorphe; imaginons de choisir pour tel domaine un anneau de centre z = 0 dont la frontière est constituée des arcs de cercle |z | = r , |z | = r , 0 麗 r 麗 r 麗 R et du segment joignant ces deux cercles et porté par le rayon qui passe par un certain point z , r 麗 |z | 麗 r . Tournant autour de la singularité z = 0 de l’angle 2 神, sur un circuit contenu dans l’anneau, partant de z et y revenant, on pourra définir la matrice: X⁺(z ) = X(ze ²ⁱ size=1^神).

On s’assure aisément que X⁺(z ) est solution locale de l’équation matricielle d X/dz = A(z )X, et, de là, qu’il existe une matrice constante non singulière U telle que X⁺(z ) = X(z ) U.

Si on définit une matrice constante B telle e ² size=1^{神i B} = U et si l’on pose Q(z ) = X(z )e size=1^{漣B ln z} , on voit que Q(ze ²ⁱ size=1^神) = Q(z ), c’est-à-dire que Q(z ) est une fonction uniforme; c’est d’ailleurs, une fonction holomorphe de z dans le voisinage de z = 0, sauf peut-être en z = 0. On obtient alors la représentation fondamentale: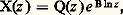

où Q(z ) est une matrice inversible fonction holomorphe de z dans 0 麗 |z | 麗 R. En outre, si¹, ...,^k sont les valeurs propres distinctes de B, 紐¹, ..., 紐^k , les sous-espaces de la décomposition spectrale, et E^j les projecteurs associés, on peut écrire la formule précédente:

Pour achever de préciser la structure de X(z ) dans le voisinage de z = 0, il faut savoir quelle est la nature du point z = 0 pour la matrice Q(z ). Or, celle-ci étant une fonction holomorphe uniforme dans le voisinage de z = 0, deux cas seuls sont possibles: elle est holomorphe en z = 0, ou bien elle a une singularité en ce point, qui ne peut être qu’un pôle ou une singularité essentielle.

On dit que le système d X/dz = A(z )X est du type de Fuchs en z = 0 si la matrice Q(z ) a au plus un pôle en ce point. Le critère de régularité de Birkhoff exprime une condition nécessaire et suffisante pour qu’il en soit ainsi: face=F0019 瑩X(z ) 瑩 憐 |z | size=1^見 doit être borné dans 0 麗 |z | 麗 R pour une certaine valeur de 見. Ces considérations s’appliquent pour la description des solutions de l’équation différentielle linéaire d’ordre n :

où les a ^j (z ) sont fonction holomorphe de z dans 0 麗 |z | 麗 R.

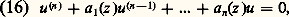Cependant, dans ce dernier cas, on peut énoncer le théorème (Fuchs): L’équation (16) est du type de Fuchs en z = 0 si et seulement si a ^j (z ) a, en z = 0, un pôle d’ordre j au plus, avec 1 諒 j 諒 n .

Le cas des équations différentielles linéaires du second ordre

D’après ce qui précède, l’équation différentielle du second ordre la plus générale qui a en z = 0 une singularité du type de Fuchs peut s’écrire:

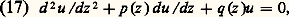avec: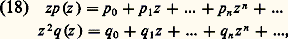

les séries p ⁿ z ⁿ , q ⁿ z ⁿ étant convergentes dans le disque |z | 麗 R. On peut chercher formellement des solutions de (17) en posant:

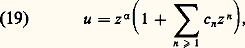見 et les c ⁿ étant des coefficients à déterminer.

Par substitution dans (17), compte tenu de (18), on peut établir que les coefficients c ⁿ sont déterminés de proche en proche de manière unique pourvu que 見 soit pris égal à l’une des racines de l’équation:

et que F( 見 + n ) ne soit jamais nul pour n entier 礪 0.

Par conséquent, si la différence des racines 見¹ 漣 見² de l’équation déterminante (20) est non nulle et non égale à un entier, on pourra ainsi obtenir deux développements du type (19) satisfaisant l’équation (17) et, dans tous les cas, on en aura au moins un.

On peut établir la convergence de ces développements par une méthode de majorante et l’on voit qu’on aura toujours une solution du type (19):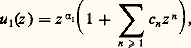

avec F( 見¹) = 0, F( 見¹ + n ) 0, n entier 礪 0, et, éventuellement, une autre solution indépendante du même type:

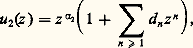si 見¹ 漣 見² n’est pas entier. Dans ce cas on dira que l’équation est du premier type de Fuchs en z = 0.

Si maintenant 見¹ 漣 見² = s , entier 閭 0, on peut faire dans (17) le changement de fonction inconnue: u = u ¹(z ) 﨣(z ) et calculer aisément 﨣(s ), ce qui conduit aux résultats suivants:

a ) s non nul:

b ) s nul: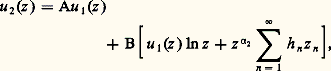

A et B désignant des constantes arbitraires.

On dira alors que l’équation est du second type de Fuchs en z = 0. Pour des raisons de commodité, nous avons discuté de la structure des solutions dans le voisinage du point singulier z = 0; mais, par le moyen d’une translation ou de la transformation z 料 1/z , on pourra toujours ramener à l’origine une singularité quelconque du plan complexe, qu’elle soit à distance finie ou infinie.

Les équations différentielles de la physique mathématique

Les équations différentielles linéaires du second ordre dont les coefficients sont fonction analytique de z , ayant pour seuls points singuliers z ¹, z ², z ³, z ⁴, et l’infini, ceux-ci étant du type de Fuchs, avec, pour exposants, 見^j , 廓^j en z ^j , 猪¹, 猪² à l’infini (racines de l’équation déterminante), sont nécessairement du type:

où A est tel que 猪¹ et 猪² sont racines de: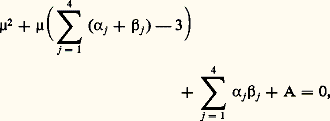

et B et C des constantes arbitraires. On notera la condition nécessaire:

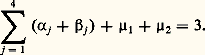Il a été établi par Klein et Bocher que de nombreuses équations différentielles qui apparaissent dans certaines branches de la physique mathématique sont des formes confluentes de l’équation spéciale de type (21) obtenue quand la différence des exposants à chaque singularité est égale à 1/2 (équation de Lamé généralisée). En général, par confluence de deux singularités, on obtient encore un point singulier du type de Fuchs, mais cela n’est plus vrai quand on envisage la confluence de trois singularités. En bref, on peut, par des confluences convenables des cinq singularités qui sont à notre disposition, obtenir six types d’équations qu’on peut classer suivant:

a) le nombre de leurs points singuliers du premier type de Fuchs avec des exposants dont la différence vaut 1/2,

b ) le nombre des autres points singuliers du type de Fuchs,

c ) le nombre de points singuliers qui ne sont pas du type de Fuchs:

Donnons un exemple: z ¹ = z ² = 0, 見¹ = 見² = 見³ = 見⁴ = 0, on fait tendre z ³ et z ⁴ vers l’infini. On obtient l’équation:

qui, par le changement de variable z 料 z ², devient l’équation de Bessel:

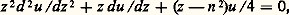
De façon analogue, l’équation différentielle linéaire du second ordre la plus générale à coefficients qui soient des fonctions analytiques de z , ayant pour seuls points singuliers a , b , c , ceux-ci étant du type de Fuchs, avec, pour exposants, 見, 見 , 廓, 廓 , 塚, 塚 , peut s’écrire (Riemann):

On exprime que u est une solution de (22) au moyen de la notation: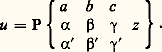

Par exemple, l’équation hypergéométrique est du type de (22):

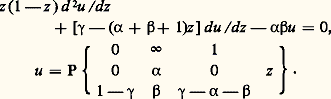Dans le cas général de l’équation de Riemann (22), les deux transformations suivantes qu’on peut vérifier par un calcul direct sont de grande importance:

où (z ¹, a ¹, c ¹) = (z , a , b , c ), égalité des rapports anharmoniques.

3. Le problème de Sturm-Liouville

Position du problème

Considérons l’équation différentielle linéaire d’ordre n :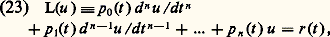

où p ⁰(t ), ..., p ⁿ (t ), r (t ) sont des fonctions continues de la variable réelle t dans l’intervalle t 捻 [a , b ], et p ⁰(t ) 0 pour t 捻 [a , b ].

Imaginons un ensemble de m conditions aux limites du type:

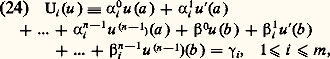où les 見^{i j} , 廓^{i j} , 塚ⁱ sont des nombres donnés, les formes linéaires (24) étant supposées linéairement indépendantes par rapport aux 2 n variables u (a ), u (a ), ..., u ^(n-1) (a ), u (b ), ..., u ^(n-1) (b ), ce qui implique m 諒 2n . On se propose de rechercher dans la classe des fonctions différentiables jusqu’à l’ordre n pour t 捻 [a , b ] s’il existe des solutions du système:

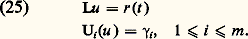Il semble commode de commencer cette étude par la discussion du problème homogène:

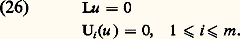Pour résoudre (26), il suffit une fois construit un système fondamental de solutions de l’équation L(u ) = 0, soit u ¹(t ), u ²(t ), ..., u ⁿ (t ), de rechercher la solution du système (26) sous la forme:

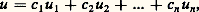les n coefficients c ¹, ..., c ⁿ devant alors être calculés par le moyen des m équations linéaires à n inconnues:

Si le rang de la matrice Uⁱ (u ^j ) est égal à p 諒 n , il existe n 漣 p vecteurs c ¹, c ² ..., c ⁿ indépendants vérifiant (27). Si le rang de cette matrice est égal à n , ce qui implique m 閭 n , le système (27) n’a pas de solution hormis la solution banale u = 0.

Des considérations analogues peuvent être développées pour le système (25).

Le système adjoint

Supposant que les coefficients p ^j (t ) ont des dérivées par rapport à t jusqu’à l’ordre n 漣 j , introduisons l’opérateur: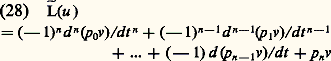

grâce auquel on obtient l’identité de Lagrange:

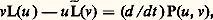où P(u , v ) est une forme bilinéaire homogène par rapport aux deux ensembles de variables u , u , ..., u ^(n-1) , et v , v , ..., v ^(n-1) . Par intégration on obtient:

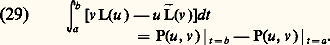Complétons le système des m formes linéaires données Uⁱ (u ) par 2n 漣 m formes linéaires des variables u (a ), ..., u ^(n-1) (a ), u (b ), ..., u ^(n-1) (b ), de telle sorte que le système des 2n formes ainsi obtenu soit encore indépendant. On peut montrer qu’il existe alors un système de 2n formes linéaires indépendantes des 2n variables v (a ), v (a ), ..., v ^(n-1) (a ), v (b ), v ^(n-1) (b ), soit V¹(v ) ... V²ⁿ (v ) tel que l’on ait l’identité:

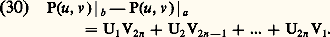Supposant U¹, U², ..., U^m fixées, remplaçons les formes U ^m+1 , ..., U ²ⁿ des mêmes variables constituant avec U¹, ..., U^m un système indépendant. Dans la formule (30), les formes V¹, ..., V^2n-m seront alors changées en des formes V ¹, ..., V ^2n-m , mais ces deux derniers systèmes de 2n 漣 m formes sont équivalents. Le système V¹ ... V^2n-m ne dépend donc en tant que système de formes linéaires, que des m formes données U¹, ..., U^m , ce qui justifie la définition suivante: Le système:

avec i = 1, 2, ..., 2 n 漣 m , est dit adjoint au système (26).

Le cas des systèmes différentiels auto-adjoints du second ordre

Un cas très important pour les applications est celui où: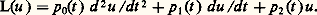

Une condition nécessaire et suffisante pour que L(u ) = 黎L(u ) est que p ⁰ = p ¹, et dans ce cas on peut écrire:

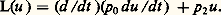Toutefois, si L(u ) n’est pas auto-adjoint, on peut le rendre tel par multiplication par un facteur convenable:

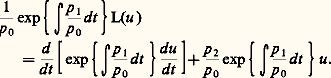Puisque, ainsi, toute équation du second ordre peut être réduite à sa forme auto-adjointe, on peut se borner à l’étude d’équation du type:

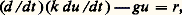connue sous le nom d’équation de Sturm-Liouville.

Étant donné le problème aux limites:

on peut construire le système adjoint: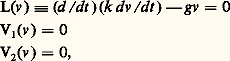

et chercher sous quelles conditions il est auto-adjoint, ce qui revient à exprimer que le système des formes U¹(u ), U²(u ) est équivalent au système V¹(u ), V²(u ). On montre qu’il en est ainsi si et seulement si:

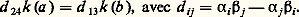Exemple:

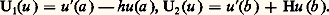Le problème de Sturm-Liouville peut être posé comme suit: étant donné l’équation

où k (t ), g (t ), r (t ) sont fonctions continues de t , k (t ) 0 pour t 捻 [a , b ] et les conditions aux limites: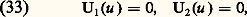

trouver les valeurs du paramètre pour lesquelles le système (32), (33) a des solutions régulières dans t 捻 [a , b ] et construire ces solutions.

La fonction de Green

Revenons au cas général de l’équation d’ordre n :

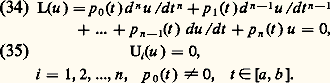On suppose le système (34), (35) incompatible, c’est-à-dire qu’il n’existe pas de solution régulière autre que la solution nulle. On peut montrer alors qu’il existe une fonction G(t , t ), dite fonction de Green, et une seule, satisfaisant aux propriétés suivantes:

1. Elle est continue et possède des dérivées continues jusqu’à l’ordre n 漣 2 inclus par rapport à t 捻 [a , b ];

2. Elle est telle que sa dérivée d’ordre n 漣 1 par rapport à t existe et est continue pour t 捻 [a , b ] sauf en t = t ; en ce point il y a discontinuité de cette dérivée, le saut valant 1/p ⁰(t );

3. Elle satisfait au système (35) et à l’équation (34) relativement à la variable t sauf en t = t .

Si H(t , t ) est la fonction de Green associée au système adjoint de (34), (35), on peut montrer que G(t , t ) = H(t , t ); en particulier, dans le cas d’un système auto-adjoint, G(t , t ) = G(t , t ) et la fonction de Green est symétrique par rapport à ses deux variables.

Si le système (34), (35) est incompatible, le système non homogène:

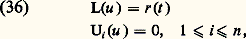a une solution unique, qu’on construit aisément avec la fonction de Green:

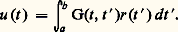Le problème aux limites de Sturm-Liouville (32), (33) est donc, sous l’hypothèse que le système homogène:

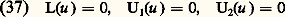soit incompatible, équivalent à l’équation intégrale:

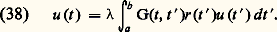Exemple de fonction de Green: soit

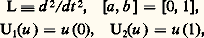on trouve:

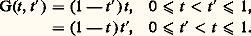Les fonctions propres et la théorie de Hilbert-Schmidt

Si le système (37) est auto-adjoint, la fonction de Green G(t , t ) est symétrique, et si l’on fait l’hypothèse r (t ) 礪 0, quel que soit t 捻 [a , b ], posant:

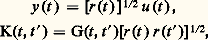l’équation (38) peut s’écrire:

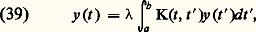où le noyau K(t , t ) est une fonction symétrique continue des deux variables t , t dans le carré t 捻 [a , b ], t 捻 [a , b ]. On est ainsi conduit à une équation intégrale de Fredholm à noyau symétrique.

Les valeurs pour lesquelles (39) a des solutions non nulles sont les valeurs propres, les solutions correspondantes étant les fonctions propres. Il est commode, pour l’énoncé des résultats, d’introduire ici la notion de produit scalaire de deux fonctions f (t ), g (t ) continues dans t 捻 [a , b ]; on notera ce produit:

où 漣g est la valeur complexe conjuguée de g ; f sera dit orthogonal à g si (f |g ) = 0.

On établit les résultats suivants (cf. espace de HILBERT, théorie SPECTRALE):

1. Toutes les valeurs propres de (39) sont réelles; deux fonctions propres qui correspondent à deux valeurs propres distinctes sont orthogonales.

2. L’ensemble des valeurs propres est dénombrable et n’a pas d’autre point limite que l’infini, éventuellement. La multiplicité de chaque valeur propre est finie, ce qui signifie que le nombre des fonctions propres linéairement indépendantes correspondant à toute valeur propre est fini.

On peut donc écrire la suite des valeurs propres: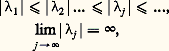

et des fonctions propres correspondantes:

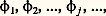si la suite est infinie, et l’on peut, grâce au procédé d’orthogonalisation de Schmidt, faire en sorte que le système des fonctions propres 﨏^j soit orthonormé, c’est-à-dire:

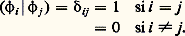3. Soit f (t ) une fonction continue de t 捻 [a , b ]. Les nombres (f | 﨏^j ), j = 1, 2, ... sont appelés les coefficients de Fourier de f .

Avec:

on a l’inégalité de Bessel:

4. Théorème de Hilbert-Schmidt . Soit f (t ) une fonction continue de t 捻 [a , b ] et:

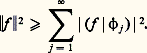
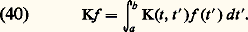Le développement de Fourier de Kf par rapport au système orthonormé de toutes les fonctions propres 﨏^j , qui s’écrit:

converge absolument vers Kf et uniformément par rapport à t 捻 [a , b ].

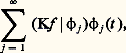Exemple: soit y (t ) une fonction continue pourvu de dérivées première et seconde continues pour t 捻 [0, 1] et telle que y (0) = y (1) = 0. Alors y (t ) satisfait à y (t ) = r (t ), r (t ) continue.

Par suite, y (t ) peut être développée en série de Fourier:

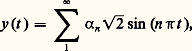avec: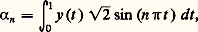

la convergence étant uniforme sur l’intervalle [0, 1]. On aura reconnu que 連2 sin (n 神t ), n = 1, 2, est le système orthogonal des fonctions propres du système y = y , y (0) = y (1) = 0.

La présentation donnée ici, qu’on a voulu très élémentaire, a été le point de départ de généralisations très importantes et très fructueuses qui sont au cœur des mathématiques contemporaines (espace de Hilbert, opérateurs linéaires, théorie spectrale, etc.). D’autre part, nous avons supposé l’intervalle [a , b ] fini et les fonctions k , g , r continues sur l’intervalle fermé, k (t ) ne s’annulant jamais. Si l’une de ces conditions est omise, les conclusions indiquées ne sont plus valables et de nouveaux problèmes apparaissent dans le détail desquels il est impossible d’entrer ici. Ces problèmes sont connus sous le nom de problèmes aux limites singuliers et les résultats fondamentaux obtenus dans ce domaine sont associés aux noms de H. Weyl, M. H. Stone, E. C. Tichmarsh, K. Kodaira, en particulier le théorème fondamental de développement qui généralise celui de Hilbert-Schmidt (spectre continu) et qui permet de donner une présentation unitaire de la théorie du développement des fonctions en série de Fourier, série de fonctions d’Hermite, fonctions de Bessel, intégrale de Fourier, etc.

Il n’est pas sans intérêt, pour conclure, de donner quelques brèves indications sur le développement historique de la question c’est-à-dire la méthode de Sturm-Liouville proprement dite.

Associons à l’équation (32) les conditions aux limites:

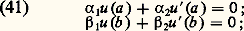on peut définir une solution de (32) satisfaisant à la première condition (41), u = u (t ,) pour t 捻 [a , b ]. Substituant dans la deuxième condition (41), on est conduit à résoudre l’équation:

On conçoit que, dans ce but, l’étude des zéros de u (t ,) dans l’intervalle [a , b ] et la manière dont ils évoluent quand varie puissent être de quelque utilité. Pour cette étude, on dispose de théorèmes de comparaison (Sturm), qui, grosso modo, indiquent comment varient ces zéros quand on remplace dans l’équation (32) k (t ) et p (t ) = r (t ) + g (t ) par des fonctions k ¹(t ) et p ¹(t ) telles que k ¹ 閭 k , p ¹ 閭 p quel que soit t 捻 [a , b ].

4. Les systèmes différentiels non linéaires

Les systèmes différentiels non linéaires dans le champ réel

On considère le système différentiel:

où x 捻 Rⁿ , f (x , t ) une fonction à valeurs dans Rⁿ , t une variable réelle. On suppose f (x , t ) définie et continue dans l’ensemble 漣G 憐 [t ⁰, t ⁰ + T], où G est un ensemble ouvert et borné dans Rⁿ .

Avec x ⁰ donné dans G, on se propose de discuter le problème aux limites: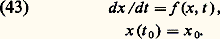

On peut imaginer le procédé constructif suivant: soit t ⁰ 麗 t ¹ 麗 t ² ... 麗 t ^p 麗 ..., une suite finie de valeurs de t et:

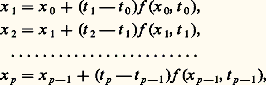et introduisons la fonction じ (t ) à valeurs dans Rⁿ définie par:

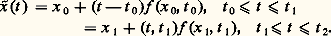La fonction じ (t ) est évidemment continue, sa représentation dans Rⁿ étant une ligne polygonale. On peut espérer, si les intervalles t ^{j + 1} 漣 t ^j ne sont pas trop grands ou mieux tendent vers 0, que x (t ) tendra d’une certaine façon vers une fonction x (t ) solution de (43).

Tel est le principe de la méthode des différences finies dont les applications débordent largement le cadre de la théorie des équations différentielles. On peut établir ainsi le théorème: Si f (x , t ) est continue dans

où G est un ensemble ouvert et borné de Rⁿ , alors pour tout x ⁰ 捻 G, il existe une fonction vectorielle x (t ) solution de (43) dans l’intervalle [t , t + h ], où: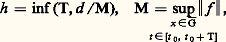

d étant la distance de x ⁰ à la frontière de G. On pourra prendre pour définition de la norme de f , ou de x , 瑩f 瑩, 瑩x 瑩, la somme des modules des composantes; on a:

On notera que cet énoncé exprime seulement l’existence d’une solution; si l’on fait l’hypothèse additionnelle:

quels que soient (x , x ) 捻 G, t 捻 [t ⁰, t ⁰ + T], où k est une constante (condition de Lipschitz), alors on peut établir qu’il y a unicité.

D’autre part, les propriétés de la solution à l’égard des conditions initiales peuvent être appréciées par le résultat suivant : si l’on suppose que f (x , t ) a des dérivées partielles premières par rapport aux composantes de x continues dans 瑩x 漣 x ⁰ 瑩 諒 嗀, t 捻 [t ⁰, t ⁰ + T], alors la solution x (t ) du système (43), qui existe et est unique dans t 捻 [t ⁰, t ⁰ + h ], a des dérivées partielles premières continues par rapport aux composantes de x ⁰.

Une autre méthode d’approche est celle des approximations successives, que nous avons déjà rencontrée. On fait l’hypothèse (44) et l’on définit la suite x ¹(t ), ..., x ^m (t ) par:

équivalente à:

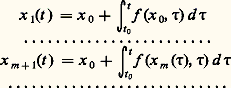On montre aisément que cette suite peut-être construite dans t 捻 [t ⁰, t ⁰ + h ] et converge uniformément dans cet intervalle vers une fonction x (t ) solution de (43); le même type d’argument permet d’établir l’unicité (cf. chap. 7 Intégration numérique des fonctions différentielles pour l’aspect numérique).

Les systèmes différentiels non linéaires dans le champ complexe

On peut développer des théorèmes d’existence locale assez voisins de ceux qui sont décrits dans le cas précédent. Mais l’étude des solutions d’un point de vue global est très instructive et amène à des distinctions intéressantes lorsqu’on discute de leurs singularités.

Celles-ci sont, en général, de deux sortes: les singularités fixes qu’on peut prévoir a priori d’après la nature du système différentiel donné et celles qui sont mobiles, c’est-à-dire dépendent des conditions initiales. Pour simplifier, on se bornera, dans l’exposé qui suit, au seul cas des équations différentielles non linéaires.

Dans le cas d’une équation du premier ordre: du /dz = f (z , u ), f fonction analytique de z et rationnelle en u , on démontre qu’il ne peut pas exister de singularité essentielle mobile, quoique des singularités mobiles plus simples puissent apparaître (pôle ou point de branchement). Exemple:

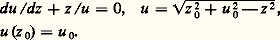Mais, dans le cas d’équation du second ordre, ou d’ordre plus élevé, des singularités essentielles mobiles peuvent apparaître comme l’indique l’exemple suivant:

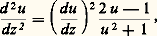qui a la solution générale:

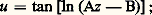A et B sont les constantes d’intégration, z = B/A est la singularité essentielle mobile.

Le problème se pose alors de déterminer s’il existe ou non des équations différentielles du second ordre:

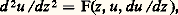où F est fonction analytique de z et rationnelle en u et du /dz telles que les points de branchement et singularités essentielles de toutes leurs solutions soient fixes.

Par une méthode de réductions successives on est conduit à cinquante types d’équations admissibles, tous étant intégrables au moyen de fonctions connues, sauf six; les équations les plus intéressantes sont, bien entendu, celles, irréductibles, au nombre de six, qui servent à définir les transcendantes de Painlevé. On se bornera à écrire les deux plus simples:

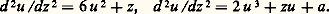On démontre que les solutions de ces équations n’ont pas de singularité essentielle ni de points de branchement mobiles. Et mêmes elles n’ont pas de point de branchement et définissent ainsi des fonctions uniformes.

5. La théorie de la stabilité

Pour la description mathématique de très nombreux systèmes physiques oscillatoires on est conduit à des équations ou systèmes différentiels dont il convient de rechercher les solutions stationnaires ou périodiques et d’étudier leurs propriétés de stabilité.

Un modèle relativement simple est fourni par l’équation: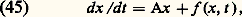

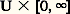où x 捻 Rⁿ , A matrice n 憐 n réelle et constante, f (x , t ) application continue de:

dans Rⁿ , U étant un voisinage de l’origine, telle enfin que f (0, t ) = 0. Il est clair que x = 0 est solution de (45) ou, comme l’on dit, un point critique. Mais que peut-on dire d’une solution dont la valeur initiale x (0) est petite? Sera-t-elle définie pour tout t 閭 0, et, dans l’affirmative, va-t-elle s’écarter notablement ou non de la solution d’équilibre x = 0. Cela amène à préciser le concept suivant de stabilité: une solution x (t ), du système dx /dt = F(x , t ) définie pour tout t 閭 t ⁰ sera dite stable si, pour tout 﨎 礪 0, il existe 嗀 = 嗀( 﨎, t ⁰) 礪 0 tel que toute autre solution y (t ) définie pour t 閭 t ⁰ et vérifiant 瑩y (t ⁰) 漣 x (t ⁰) 瑩 諒 嗀 satisfait à 瑩y (t ) 漣 x (t ) 瑩 諒 﨎 pour t 閭 t ⁰.

Si, de plus, y (t ) 漣 x (t )0 quand t+ 秊, on dira que la solution x (t ) est asymptotiquement stable.

On observera que, pour discuter la stabilité d’une solution x (t ) d’un système quelconque dx /dt = F(x , t ), on pourra toujours, par le changement x = x (t ) + y , se ramener à l’étude de la stabilité d’une solution stationnaire d’un système différentiel, ce qui justifie l’importance de système du type (45).

Revenant à ce cas, on peut énoncer le théorème (Poincaré-Liapounoff): Si les valeurs propres de la matrice A ont toutes leur partie réelle négative et si la fonction f (x , t ) continue dans 瑩x 瑩 諒 福, t 閭 0 est telle que:

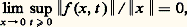x = 0 est solution asymptotiquement stable de (45).

Si l’une au moins des valeurs propres de A est à partie réelle positive, la solution x = 0 est instable.

Le théorème de stabilité demeure vrai si la matice A est une fonction continue périodique de t dont tous les coefficients caractéristiques sont à partie réelle négative.

Le problème fondamental de la stabilité de la solution x = 0 du système:

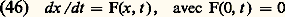peut être abordé par la méthode directe de Liapounoff.

Pour en expliquer le contenu, il faut donner quelques notations préliminaires: on dira que la fonction scalaire V(x , t ) a un signe constant si, dans un domaine 行(a , 精 ): face=F0019 瑩x 瑩 諒 a , t 閭 精, convenable, elle est différentiable, ne prend que des valeurs d’un même signe ou nulle et V(0, t ) = 0; elle sera dite positive ou négative selon la nature de ce signe.

Si W(x ) est une fonction scalaire indépendante du temps, on dira que W(x ) est définie positive (ou définie négative) si elle est différentiable, et est positive (ou négative) dans un 行(a , 精) convenable et ne s’annule qu’à l’origine. La fonction scalaire V(x , t ) sera dite définie positive (ou définie négative) s’il existe une fonction définie positive W(x ) telle que V 漣 W (ou 漣 V 漣 W) est positive dans un 行(a , 精) et V(0, t ) = 0.

Supposant que F(x , t ) est continue dans un 行(a , 精) convenable, on a les théorèmes suivants:

– Si, pour le système (46) et dans un domaine 行(a , 精), il existe une fonction définie V(x , t ) dont la dérivée:

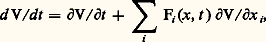est d’un signe constant opposé, alors x = 0 est solution stable de (46).

– Si, pour le système (46) et dans un domaine 行(a , 精), V(x , t ) et d V/dt sont définies et de signe contraire et si

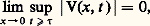alors x = 0 est une solution asymptotiquement stable de (46).

– Si, pour le système (46), on a pu construire une fonction V(x , t ) telle que:

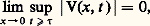d V/dt soit définie (positive ou négative) dans 行(a , 精), et que, pour chaque valeur t 礪 精 et chaque 兀 礪 0 aussi petit qu’on veut, V et d V/dt peuvent avoir, en certain point de 瑩x 瑩 麗 兀, le même signe, alors x = 0 est solution instable du système (46).

La difficulté d’application de ces théorèmes réside, bien entendu, dans la construction des fonctions de Liapounoff; aussi de nombreux efforts ont été tentés visant, d’une part, à assouplir les conditions imposées dans l’espoir de rendre plus facile cette construction, d’autre part, à reconnaître parmi ces conditions celles qui sont nécessaires pour tel type de stabilité.

Voici, pour conclure, un exemple d’application. Soit le système:

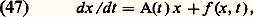où A(t ) est une matrice n 憐 n fonction réelle continue et bornée dans t 閭 0, f (x , t ) application à valeurs dans Rⁿ , continue dans 瑩x 瑩 諒 a , t 閭 0, et telle que

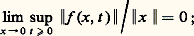s’il existe une fonction de Liapounoff pour l’approximation linéaire dx /dt = A(t )x , c’est-à-dire une fonction V(x , t ) satisfaisant pour ce système linéaire aux exigences du troisième théorème énoncé plus haut, alors x = 0 est une solution asymptotiquement stable de (47).

6. Les solutions périodiques des systèmes différentiels

Un problème très important pour certaines applications est la recherche de solution périodique de système du type dx /dt = f (x , t ), où f (x , t ), application continue dans Rⁿ , est supposée périodique par rapport à la variable réelle t de période T (cas non autonome), ou encore du type dx /dt = f (x ) (cas autonome).

On ne dispose d’aucune méthode d’investigation assez puissante pour répondre à ces questions de manière générale. Les méthodes existantes sont de deux sortes. Les unes, méthode de perturbation, méthode de centrage, permettant l’étude de systèmes quasi linéaires, c’est-à-dire de systèmes dans lesquels la partie non linéaire apparaît multipliée par un paramètre qu’on suppose petit; le calcul de représentations asymptotiques des solutions périodiques est généralement possible, ainsi que l’étude de la stabilité de ces solutions. Les autres sont des méthodes topologiques qui fournissent pour certains systèmes fortement non linéaires des résultats d’existence de solutions périodiques.

La méthode des perturbations (H. Poincaré)

Considérons l’équation:

où x est une fonction scalaire, x = dx /dt , x = d ²x /dt ², f fonction périodique de t de période 2 神/ 諸 et 猪 un petit paramètre, tous les éléments ainsi définis étant réels.

Quand 猪 = 0 l’équation se réduit à x + x = 0 qui a pour solution générale x = a cos(t + 﨏), périodique de période 2 神, a et 﨏 désignant des constantes arbitraires.

Supposons que 諸 est voisin de l’unité ou mieux que 諸^-2 = 1 漣 猪兀, 兀 étant une fonction donnée de 猪 analytique dans le voisinage de 0,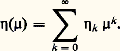

Pour chercher si l’équation (48) a des solutions périodiques de période 2 神/ 諸, nous posons 諸 t = + 嗀, nouvelle variable, 嗀 paramètre de translation. Il vient ainsi:

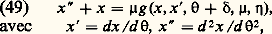et: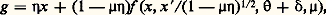

et l’on recherche une solution périodique de (49) de période 2 神 en , telle que x (0) = a , x (0) = 0 (cette condition initiale fait comprendre le rôle du paramètre de translation 嗀). La théorie de Poincaré montre que si a et 嗀⁰ sont solution réelle du système d’équations:

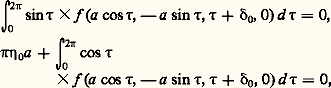telle que:

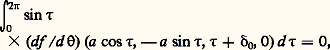et si g (x , x , + 嗀, 猪, 兀) continue par rapport à tous ses arguments peut être développée en série de puissances de x 漣 a cos , x + a sin , 猪, 兀 漣 兀⁰, 嗀 漣 嗀⁰ convergente pour tout si tous ces arguments sont de module moindre qu’un nombre positif 福, alors il existe une solution périodique de l’équation (48) que l’on peut représenter par la série:

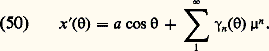Celle-ci peut être dérivée terme à terme deux fois, et:

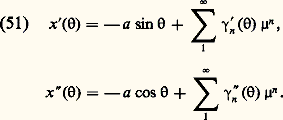On peut représenter 嗀 par une série:

et l’on peut obtenir les développements (50) et (52) par substitution dans l’équation (49) et identification dans les deux membres des coefficients des mêmes puissances de 猪. On obtient ainsi un système récurrent:

On détermine les 塚ⁿ ( ) et les coefficients 嗀^k en imposant aux fonctions 塚ⁿ la condition de périodicité par rapport à de période 2 神 et en plus: 塚ⁿ (0) = 塚 ⁿ (0) = 0.

Cette méthode de calcul appliquée à l’équation de Duffing: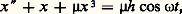

avec 諸^-2 = 1 漣 猪兀, h constante, conduit à:

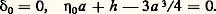On peut donc obtenir trois solutions périodiques, et en tout cas au moins une; on a la représentation:

.

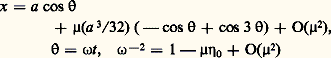La théorie qui précède permet de donner une description satisfaisante du phénomène de synchronisation des oscillateurs quasi linéaires. Si l’oscillateur linéaire est attaqué par une force périodique non linéaire de période voisine de sa période propre, il y a synchronisation sur la force excitatrice, l’oscillation ayant en outre une amplitude bien définie.

La théorie de Poincaré permet aussi de rendre compte du phénomène de démultiplication de fréquence, c’est-à-dire l’existence de solutions sous-harmoniques, périodiques de période multiple de celle de la force excitatrice. Ces résultats d’une grande importance théorique et pratique sont spécifiques de la non-linéarité.

Le cas des systèmes autonomes peut être traité de façon similaire; considérons par exemple l’équation:

et proposons-nous de chercher s’il existe une solution périodique de (53) qui, lorsque 猪0, tend vers une solution bien déterminée de x + x = 0, périodique de période 2 神. Cela suggère que la période de la solution cherchée 2 神/ 諸 peut être représentée par 諸^-2 = 1 漣 猪兀, où 兀( 猪) est une fonction de 猪 qui, à la différence du cas précédent, est une inconnue du problème. Avec cette représentation et la nouvelle variable 諸 t = , l’équation devient: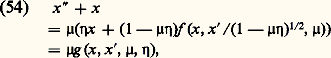

dont il convient de rechercher une solution périodique de période 2 神. On peut alors démontrer suivant la méthode de Poincaré que si a ⁰ et 兀⁰ sont des nombres réels satisfaisant aux équations:

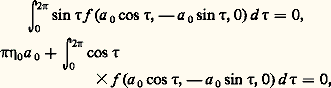tels que:

Si, en outre, g (x , x , 猪, 兀) peut être développé en série de puissances de x 漣 a ⁰ cos , x + a ⁰ sin , 猪, 兀 漣 兀⁰ convergente lorsque ces quantités sont de module assez petit, alors il existe une fonction 兀( 猪) pour laquelle (54) possède une solution périodique x ( ) de période 2 神 telle que x (0) = a ⁰, x (0) = 0, qu’on peut représenter par les séries: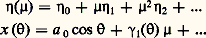

Le développement de x ( ) peut être dérivé terme à terme deux fois et l’on peut obtenir les coefficients de ces séries par substitution dans (54) et identification dans les deux membres des termes de même puissance en 猪.

La détermination de 塚ⁿ ( ) et 兀^k se fait alors par un procédé récurrent: 塚 ⁿ + 塚ⁿ = 﨏( 塚¹, ..., 塚^n-1 , 兀¹ ..., 兀^n-1 ) et les conditions 塚ⁿ (0) = 0, 塚 ⁿ (0) = 0, avec 塚ⁿ ( ) périodique de période 2 神.

Appliquant ces considérations à l’équation de Van der Pol:

on trouve ainsi:

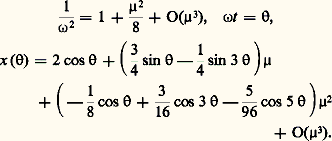La méthode de centrage (Kryloff-Bogoliuboff-Haag)

a ) Considérons le système:

avec x 捻 Rⁿ , f application à valeurs dans Rⁿ , périodique par rapport à t de période T et pourvue de dérivées partielles premières continues. L’idée fondamentale est de substituer à (55) l’équation:

On peut établir que les solutions x (t ) et じ (t ) respectivement de (55) et (56) qui prennent pour t = 0 même valeur demeurent assez voisines sur un intervalle de temps d’autant plus grand que 猪 est plus petit. De manière plus précise, sous certaines hypothèses, on établit qu’il existe une fonction croissante h (t ) telle que: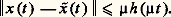

Ce résultat signifie essentiellement que, choisissant 猪 assez petit, l’écart entre les solutions sera moindre qu’un nombre donné 﨎 sur un intervalle de temps qui sera de l’ordre de 猪^-1, donc très grand si 猪 est petit:

pour t 捻 [0, L/ 猪] et a fortiori pour t 捻 [0, Lh (L)/ 﨎],

b ) D’un autre côté, cette méthode permet de prévoir aussi l’existence de solutions périodiques et d’étudier leur stabilité.

Plus précisément, on a le théorème: Si a 捻 Rⁿ est tel que F(a ) = 0, et si la matrice:

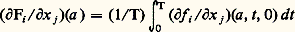est non singulière, alors le système (55) possède une solution périodique de période T pour 猪 assez petit, qui, lorsque 猪0, tend uniformément vers a ; de plus, si les valeurs propres de cette matrice ont toutes leurs parties réelles négatives, la solution périodique mise en évidence est asymptotiquement stable.

De nombreuses extensions sont possibles et pour conclure nous citerons un résultat fondamental: soit le système quasi linéaire:

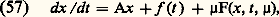où A est une matrice réelle n 憐 n constante, f (t ) et F(x , t , 猪) des applications dans Rⁿ périodiques en t de période T, F pourvue de dérivées partielles du premier ordre continues.

Si aucune valeur propre de la matrice A n’est égale à 梁 2 神 iq /T, q entier, alors pour 猪 assez petit, le système (57) a une solution périodique unique de période T, asymptotiquement stable si les valeurs propres de A sont toutes à partie réelle négative.

Si certaines valeurs propres de A sont multiples de 梁 2 神 i /T, alors le système dx /dt = Ax possède un système maximal de solutions périodiques de période T, 﨏^(j) (t ) de composantes 﨏^ij (t ) avec 1 諒 j 諒 m 諒 n . Le système adjoint: dx /dt + ^t Ax = 0 (^t A matrice transposée de A) possède aussi un système maximal de m solutions périodiques de période T, 祥^(k) (t ) de composantes 祥^ik (t ), qu’on peut toujours supposer construit de telle sorte que: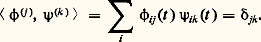

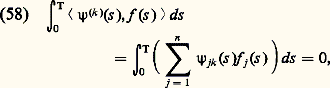Le système linéaire non homogène dx /dt = Ax + f (t ), sous réserve que l’on ait:

pour 1 諒 k 諒 m , possède alors une famille de solutions périodiques de période T, qu’on peut écrire:

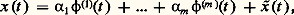où les 見ⁱ sont des constantes arbitraires.

Revenant au système (57), on écrit les équations:

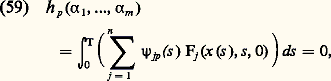avec 1 諒 p 諒 m , on suppose qu’il existe un système de valeurs réelles 見¹⁰, ..., 見^m0 solution des équations (59) telles que le jacobien:

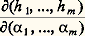ne soit pas nul pour cet ensemble de valeurs.

Alors le théorème de Malkin affirme que, sous réserve des conditions (58), pour 猪 assez petit, le système (57) possède une solution périodique de période T qui, lorsque 猪0 tend vers:

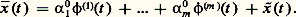Il est généralement possible de déterminer les termes suivants du développement asymptotique de la solution par rapport à 猪 et d’en étudier la stabilité.

Ajoutons, pour conclure, que ces méthodes permettent aussi de discuter du cas des systèmes autonomes, et que d’importantes généralisations sont possibles, en particulier pour l’étude des systèmes presque périodiques.

Les méthodes topologiques

Considérons le système différentiel:

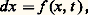avec f à valeurs dans Rⁿ , périodique en t de période T. Sous certaines conditions, on peut définir la solution x (t ; x ⁰) de (59), qui, pour t = 0, prend la valeur x ⁰, valable pour t 捻 [0, T].

Définissant l’opérateur 溜x ⁰ = x (T; x ⁰) de Rⁿ dans Rⁿ , l’on voit que, pour obtenir une solution périodique de période T de (59), le problème fondamental consiste à trouver un point fixe de cet opérateur, c’est-à-dire x ⁰ tel que: x ⁰ = 溜x ⁰.

On peut présenter cette idée de manière différente; proposons-nous, par exemple, de rechercher la solution périodique de période T du système:

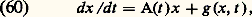où A(t ), g (x , t ) sont respectivement matrice n 憐 n , applications dans Rⁿ périodiques en t de période T. On suppose que le système homogène:

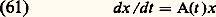n’a pas de solution périodique de période T.

On introduit, pour le système matriciel:

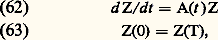une matrice n 憐 n , G(t , t ) (matrice de Green) satisfaisant aux propriétés suivantes: G(t , t ) vérifie (62) pour 0 諒 t 麗 t et t 麗 t 諒 T, satisfait à (63) relativement à t , enfin est discontinue en t = t avec un saut:

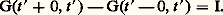Si X(t ) est la matrice résolvante de (62) alors X(T) 漣 I est inversible (car (61) n’a pas de solution périodique T) et l’on peut montrer que:

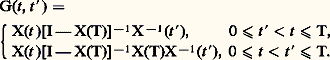On s’assure facilement que toute solution périodique de période T de (60) est solution de l’équation intégrale non linéaire:

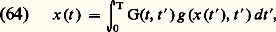et inversement.

Si l’on considère le second membre de (64) comme un opérateur 溜 agissant sur l’espace des fonctions continues x (t ), t 捻 [0, T], on voit que le problème consiste à trouver un point fixe de cet opérateur, c’est-à-dire une fonction continue x (t ) telle que x = 溜x .

La théorie des points fixes des opérateurs non linéaires a reçu dans les dernières décennies un développement considérable et a rendu possible la recherche de solutions périodiques de systèmes différentiels dans de nombreux cas.

Nous allons, pour conclure, ajouter quelques développements dans le cas des systèmes autonomes de dimension 2.

Soit le système:

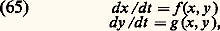x , y , variables scalaires, f , g , fonctions réelles continues au sens de Lipschitz dans un ensemble D ouvert et borné du plan x , y .

Si C⁺ (ou C^-) est une semi-orbite de (65), c’est-à-dire l’ensemble des points P(t ) dont les coordonnées sont 﨏(t ), 祥(t ), solution de (65) définie dans t 閭 t ⁰(t 諒 t ⁰) pour un certain t ⁰, un point Q du plan sera dit point limite de C⁺ (ou de C^-) s’il existe une suite de nombres réels t ⁿ , t ⁿ+ 秊(t ⁿ漣 秊) telle que P(t ⁿ )Q, si n秊. L’ensemble de tous les points limites d’une semi-orbite C⁺ (ou C^-) est désigné par (L(C⁺) L(C^-)), et L(C) = L(C⁺) 聆 L(C^-) est l’ensemble limite de l’orbite.

On a les théorèmes suivants:

– Si C⁺ est une semi-orbite contenue dans un ensemble fermé K 說 D, alors L(C⁺) est non vide, fermé et connexe.

Définition. Les points de D en lesquels f et g s’annulent sont les points critiques; tout autre point de D sera dit régulier.

– Soit C⁺ une semi-orbite positive contenue dans un sous-ensemble fermé K 說 D et supposons que L(C⁺) contienne un point régulier Q. Alors L’orbite C^Q passant par Q existe en tant qu’orbite complète t 捻 ] 漣 秊, + 秊 [ et C^Q 說 L(C⁺).

– Soit C⁺ une semi-orbite positive contenue dans un sous-ensemble fermé K 說 D. Si L(C⁺) se compose exclusivement de points réguliers, alors C⁺ (= L(C⁺)) est une orbite périodique ou L(C⁺) est une orbite périodique; dans le second cas, on dit que L(C⁺) est un cycle limite.

– Corollaire (théorème de Poincaré-Bendixson ). Si C⁺ est une semi-orbite contenue dans un sous-ensemble compact K 說 D, dans lequel il n’y a pas de point critique, alors K contient une orbite périodique.

Si T est la période et si:

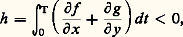cette intégrale étant calculée sur le cycle, celui-ci est asymptotiquement stable.

Voici, pour conclure, l’exemple suivant (équation de Liénard): x + x = f (x ), qu’on écrira:

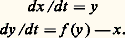On suppose f (y ) pourvue d’une dérivée continue et telle que f (y ) = g (y ) 漣 見y , 見 constante avec dg /dy 礪 0, dg/dy (0) 礪 見, g ( face=F0019 漣 y ) = 漣 g ( face=F0019 漣 y ), |g (y )| 麗 c , c constant; le théorème de Poincaré-Bendixson peut être utilisé dans ce cas pour mettre en évidence un cycle limite.

Soit E un espace topologique; un système dynamique est une famille d’opérateurs F^t (t 捻 R) de E dans E possédant les propriétés suivantes:

a ) ⁰ est l’opérateur identité,

b ) pour tous t ¹, t ² réels F^{t 1 + t 2} = F^{t 1}F^{t 2},

c ) l’élément F^t p de E dépend continûment de (p , t ) 捻 E 憐 R.

En particulier si l’on prend pour E l’espace Rⁿ et si f (x , t ) est une fonction continue de Rⁿ 憐 R dans Rⁿ , lipschitzienne en x , on peut définir x (t , x ⁰) la solution unique du système: dx /dt = f (x , t ), x (0, x ⁰) = x ⁰, puis la famille d’opérateurs F^t : RⁿR définie par F^t (x ⁰) = x (t , x ⁰), laquelle constitue un système dynamique au sens de la définition donnée plus haut.

L’étude des systèmes dynamiques ^{[cf. SYSTÈMES DYNAMIQUES DIFFÉRENTIABLES]} constitue donc un prolongement naturel de la théorie des équations différentielles et a donné lieu à de nombreux travaux: problèmes de stabilité, problèmes ergodiques (cf. théorie ERGODIQUE), etc.

Une autre généralisation importante consiste à considérer des équations différentielles dans lesquelles la fonction inconnue a des valeurs dans un espace métrique, par exemple un espace de Hilbert ou un espace de Banach.

On peut ainsi discuter des équations du type:

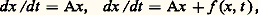où x est pour toute valeur réelle de t élément d’un espace de Banach E, A désignant un opérateur linéaire de E dans E, f (x , t ) application non linéaire de E 憐 R dans E.

Dans le cas où l’opérateur A est indépendant de t , sous certaines conditions additionnelles, l’étude de l’équation dx /dt = Ax conduit à la théorie bien développée des semi-groupes d’opérateurs dans E. Le cas des équations non linéaires a été aussi considéré en liaison avec les problèmes d’évolution, la question se posant, en général, de savoir comment se comportent pour t+ 秊 les solutions de tels systèmes.

Le développement considérable de l’analyse fonctionnelle a beaucoup contribué aux progrès de ces théories dont l’étude se poursuit activement.

7. Intégration numérique des équations différentielles

Méthode d’Euler

Prenons d’abord le cas d’une équation différentielle du 1^er ordre: Trouver y , fonction d’une variable x , dérivable sur [x ⁰, x ⁰ + a ] = I, telle que, f désignant une fonction continue sur I 憐 R,

pour tout x 捻 I, et:

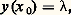où est donné dans R.

L’idée est de remplacer le problème théorique précédent, noté P, par le problème discrétisé Pⁿ suivant (méthode d’Euler): Trouver Yⁿ = (y ⁰, y ¹, ..., y ⁿ ), suite finie de n + 1 nombres réels telle que:

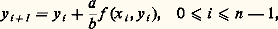où:

ce problème Pⁿ est obtenu en divisant I = [x ⁰, x ⁰ + a ] en n parties égales avec un pas égal à h = a /n et en cherchant une approximation y ⁱ de y (x ⁱ ) où y est la solution (lorsqu’elle est unique) de P¹.

Le raisonnement, fort simple, est le suivant: Si y est solution unique de P¹, y (x ⁱ ) est proche de:

et donc, si y ⁱ est «proche» de y (x ⁱ ), on peut remplacer P¹ par Pⁿ .

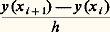Pⁿ est un problème discrétisé associé à P¹. On remarque alors immédiatement qu’une notion importante va devoir être précisée: comment dire que la solution de Pⁿ converge vers celle de P¹ lorsque n tend vers + 秊. L’analyse numérique devra fournir des majorations pour |y (x ⁱ ) 漣 y ⁱ |.

Dans la suite, nous supposerons toujours que f satisfait à la condition (L) suivante appelée condition de Lipschitz globale : il existe L 閭 0 tel que:

pour tout x 捻 I, u 捻 R et v 捻 R.

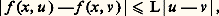Cette condition assure l’existence et l’unicité du problème P (cf. chap. 4).

On peut espérer que, si h est assez petit, le nombre y ⁱ est proche de y (x ⁱ ). C’est pourquoi le nombre e ⁱ = y (x ⁱ ) 漣 y ⁱ sera appelé l’erreur au point x ⁱ , tandis que:

est l’erreur globale aux points x ⁱ , 0 諒 i 諒 n .

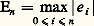Le procédé P^h est dit convergent si:

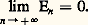Notons que cette notion de convergence est peu habituelle; car la solution de P est une fonction x 料 y (x ), alors que la solution Yⁿ de Pⁿ est une suite finie de n + 1 nombres réels. Ainsi, y et Yⁿ n’appartiennent pas au même espace et nous ne pouvons pas mesurer une distance éventuelle de y à Yⁿ . Néanmoins, cette notion de convergence satisfait le physicien, qui ne cherche pas explicitement y mais qui veut surtout des valeurs approchées de y (x ⁱ ) pour un certain pas h . Si Eⁿ est petit, l’erreur de discrétisation provoquée par le passage de P à Pⁿ est faible.

Théorème . Si (L) est satisfaite, le procédé Pⁿ est convergent. Plus précisément, on peut montrer que:

où les maximums sont pris pour t ¹ 捻 I, t ² 捻 I, avec |t ¹ 漣 t ²| 諒 h .

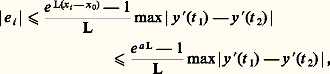Cette majoration prouve la convergence; car, f étant continue, la solution unique de P possède une dérivée continue sur I, donc uniformément continue, de sorte que le maximum y (t ¹) 漣 y (t ²), pour |t ¹ 漣 t ²| 諒 h , tend vers 0 avec h .

Néanmoins, cette majoration ne donne pas de bornes pour l’erreur commise, car elle fait intervenir la dérivée de la fonction inconnue.

Cherchons une majoration de Eⁿ . Prenons tout d’abord (L) comme seule hypothèse. On peut alors montrer que la solution unique de P satisfait à:

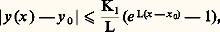où: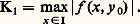

Une majoration de K¹ est en général assez simple à déterminer, de sorte qu’on peut définir un ensemble borné 阮 de I 憐 R qui contient (x , y (x )) tel que y soit solution de P. C’est l’ensemble 阮, défini par:

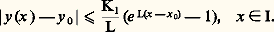Si, sur 阮, qui est un ensemble borné fermé, la fonction f possède des dérivées partielles continues:

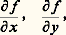on peut alors majorer |e ⁱ | par:

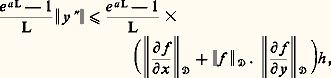Remarquons que cette majoration est utilisable si on peut calculer aisément:

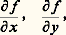et si on peut majorer simplement: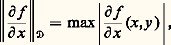

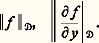où le maximum est pris pour (x , y ) 捻 阮, et de même pour:

Le résultat final est alors:

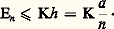Ainsi, la convergence est en 1/n . On peut l’accélérer par la méthode d’extrapolation à la limite (méthode de Richardson, ou encore de Romberg; cf. approximation et représentation des FONCTIONS).

La méthode d’extrapolation à la limite est très facile à appliquer. On peut, par exemple, diviser I en n parties égales, prendre pour x = x ^{i ,0} un des points de subdivision, puis diviser en 2n parties égales en écrivant x = x ⁱ⁽¹⁾ , puis en 4n partie égales en posant x ⁱ⁽²⁾ = x , puis en 2^p n parties égales en posant x ^i(p) = x .

On résout alors les p schèmes:

et on obtient y ^i(k) pour 1 諒 k 諒 p .

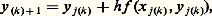Si f est suffisamment différentiable sur 阮, les conditions d’application de l’extrapolation à la limite sont satisfaites et on peut remplacer y ^i(p) par une moyenne convenable:

telle que 黎y ^i(p) converge vers y (x ) plus vite que y ^i(p) lorsque p tend vers + 秊.

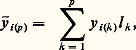Une famille de méthodes numériques

Nous avons jusqu’ici remplacé P par Pⁿ :

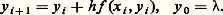Nous proposons maintenant une généralisation de ce procédé: cette généralisation n’a pas pour unique objet de généraliser, elle prétend permettre d’aboutir à des méthodes plus efficaces que la méthode d’Euler.

Dans P intervient une fonction et f un nombre. Dans la méthode d’Euler, Pⁿ faisait intervenir la même fonction f et le même nombre. Associons ici à f une fonction f ⁿ et à un nombreⁿ , et remplaçons le problème P par le problème Pⁿ . Pour le moment, f ⁿ est une fonction donnée, définie sur I 憐 R, et dépendant du paramètre h .

Considérons le problème P^h : Trouver Yⁿ = (y ⁰, ..., y ⁿ ) tel qu’on ait:

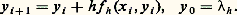Faisons une étude de la convergence et essayons de choisir^h et f ^h pour que l’«ordre de convergence» (cf. infra ) soit bon.

Consistance

Nous dirons que le procédé P^h est consistant par rapport à P si:

Cette condition est relativement simple à vérifier et assez intuitive: f ^h doit «ressembler à f , pour h suffisamment petit». Par exemple, dans la méthode d’Euler, on avait f ^h = f , pour tout h , et cette méthode était donc trivialement consistante par rapport à P.

S’il en est ainsi, on peut démontrer que, pour toute solution y de y = f (x , y ), on a, avec h = a /n ,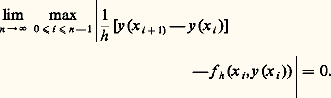

Remarquons que cette notion ne fait intervenir que les f ^h et non les^h .

Stabilité

Considérons les deux problèmes définis par la même équation y = f (x , y ) et par les données initiales y (x ⁰) = d’une part, et y (x ⁰) = d’autre part. Supposons que (L) soit satisfaite. Les deux problèmes précédents possèdent respectivement une solution y et une solution 泌 . Il peut arriver que, même lorsque | 漣| est faible, la quantité:

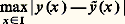soit grande. C’est un phénomène d’instabilité du problème posé (indépendamment de toute méthode numérique de résolution). Ce phénomène d’instabilité est très gênant, car, si = 神 par exemple, toute méthode numérique remplacera 神 par = 3,141 59... avec un nombre fini de décimales. Nous retrouverons évidemment cet ennui de résolution théorique dans la résolution numérique. Cela nous conduit à la définition suivante.

Un procédé P^h défini par f ^h et^h est dit stable si, pour toute matrice triangulaire infinie ( 﨎ⁱⁿ ), 0 諒 i 諒 n 漣 1, telle que:

il existe des constantes K¹ et K² telles que:

où y ⁱ et z ⁱ , 0 諒 i 諒 n , sont solutions de:

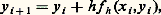avec y ⁰ quelconque, et de:

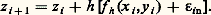Cette condition de stabilité exprime le fait qu’une légère variation, sur les données initiales y ⁰ et z ⁰ d’une part, sur f ^h d’autre part, n’entraîne pas de grosses variations sur les résultats obtenus en résolvant P^h . La condition de stabilité n’est pas simple. Voici une condition suffisante: le procédé P^h est stable s’il existe 炙 礪 0 tel que:

pour tous x 捻 I, u 捻 R, v 捻 R et h 捻 [0, h ⁰]; donc 炙 est indépendant de x , y , v et h . Nous admettrons ce résultat.

Convergence

Considérons les problèmes P et P^h suivants: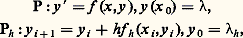

admettant pour solutions respectives les fonctions y 捻 暈¹(I) et Yⁿ = (y ⁰, ... y ⁿ ). Nous dirons que le schéma P^h est convergent si:

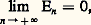où: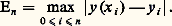

Théorème fondamental de convergence . Si le schéma P^h est stable d’une part, et consistant par rapport à P d’autre part, le schéma P^h est convergent, à condition que:

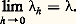En effet, comme P^h est consistant par rapport à P, on peut écrire:

où y est la solution de P et où:

tend vers zéro lorsque n tend vers + 秊.

En posant z ⁱ = y (x ⁱ ), on a:

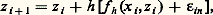de sorte que, par la condition de stabilité, on obtient:

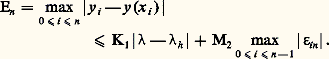Si^h tend vers, on a:

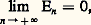Ordre d’une méthode

Nous venons de voir que, si:

alors, le procédé P^h défini par f ^h est stable et consistant, donc convergent: cela prouve simplement que:

Nous dirons qu’une méthode est d’ordre p si on a Eⁿ 諒 Kh ^p lorsque^h =. Des conditions pour qu’une méthode soit d’ordre p ont été données: elles font intervenir les dérivées par rapport à h de la fonction h 料 f ^h (x , y ) = g (h ). Les techniques utilisées sont relativement simples: il suffit de faire un usage fréquent de la formule de Taylor. Contentons-nous de donner certains résultats.

Supposons que f est p fois continûment différentiable. Posons:

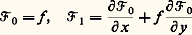et, de proche en proche,

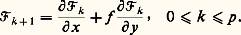Il en résulte que, si y est solution de P, on a:

Pour que le procédé P^h soit d’ordre p , il suffit que: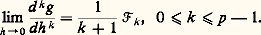

La méthode du développement de Taylor consiste à prendre:

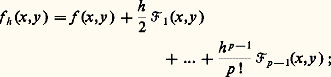on peut alors démontrer que Eⁿ 諒 Kh ^p . Cette méthode est cependant assez difficile à utiliser car elle nécessite le calcul effectif des 杻^k .

On peut aussi écrire:

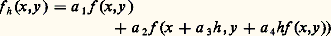et on cherche a ¹, a ², a ³, a ⁴ pour que la méthode soit d’ordre aussi élevé que possible. En écrivant que:

on obtient les conditions a ¹ = 1 漣 見, a ² = 見, a ³ = a ⁴ = 1/(2 見).

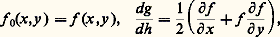Pour 見 = 1/2, on a la méthode de Heun :

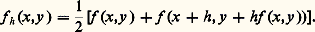Pour 見 = 1, on a la méthode d’Euler améliorée :

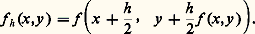Indiquons enfin la méthode de Runge et Kutta ; on pose:

avec:

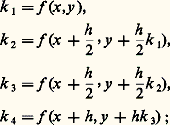cette méthode est d’ordre 4.

Méthode des approximations successives

On sait que le problème P est équivalent au problème Q: Trouver y continu sur I tel que:

Si y est solution de Q, et donc de P, on a: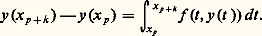

Supposons connues des valeurs approchées y ^p-q ,..., y ^p de y (x ^p-q ), ..., y (x ^p ). Nous connaissons alors des valeurs approchées de: f (x ^p-j , y (x ^p-j )), 0 諒 j 諒 q . Posons:

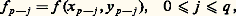et considérons le polynôme d’interpolation sur les points x ^p-q , ..., x ^p de la fonction t 料 f (t , y (t )) dont nous connaissons des valeurs approchées f ^p-j aux points x ^p-j . Le calcul approché de:

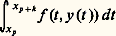peut se faire par une formule d’intégration de type ouvert, n’utilisant que les points précédant x ^p et le point x ^p .

On a, par exemple, la formule approchée:

où P désigne le polynôme d’interpolation sur les points x ^p-q , ..., x ^p .

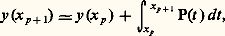Considérons donc le schéma ou algorithme défini par la méthode d’intégration de Newton-Gregory:

où les différences régressives sont définies à partir de:

par récurrence:

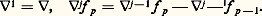Ce schéma nous permet de calculer y ^p+1 , pour p = q , puisque les 暴^j f ^q sont connus; y ^q+1 étant connu, nous calculons y ^q+2 en changeant p en p + 1 et ainsi de suite, en utilisant toujours le même nombre q + 1 de points qui précèdent x ^p+1 . Le problème qui se pose est alors de savoir si les y ^p ainsi calculés sont proches des valeurs y (x ^p ) de la solution exacte.

L’algorithme précédent est dit explicite; car, à chaque étape, il définit une inconnue y ^p+1 explicitement. La méthode suppose connues les valeurs de départ y ⁰, ..., y ^q qui sont des valeurs approchées de y (x ⁰), ..., y (x ^q ) et qui ont donc été obtenues par une autre méthode, par exemple une méthode à un pas, alors qu’ici nous obtenons y ^q+1 par une méthode utilisant y ⁰, ..., y ^q , et c’est pourquoi nous dirons que la méthode précédente est une méthode multipas, à q pas exactement.

Remarquons que les c ^j peuvent être déterminés par la méthode de la fonction génératrice introduite à propos de l’intégration numérique par la méthode de Newton-Gregory.

On peut aussi utiliser la méthode suivante. On calcule:

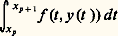de façon approchée par une formule de type fermé qui utilise donc y ^p+1 que l’on cherche. Le schéma s’écrit:

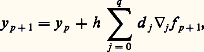où les d ^j peuvent aussi être calculés par la méthode de la série génératrice.

Cette équation s’écrit encore sous la forme:

où K^p ne dépend que des point x ^p-k , pour k 閭 0.

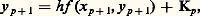On obtient donc y ^p+1 implicitement; mais, p étant fixé, la détermination de y ^p+1 peut être faite par itération: on prend la valeur y ^0p+1 obtenue par le schéma explicite et on itère en écrivant:

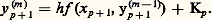La suite des y ^{(m) p+1} , pour m = 0, 1, 2, 3, ..., converge vers la solution y ^p+1 du schéma implicite lorsque h est suffisamment petit; car, si on écrit le schéma implicite sous la forme y ^p+1 = 淋(y ^p+1 ), on a:

Donc on a la majoration:

et la convergence est assurée si h L 麗 1.

La première méthode explicite permet de définir une première approximation de y ^q+1 : nous dirons que c’est une formule de prédiction . La deuxième méthode permet de modifier le résultat précédent et de l’améliorer: c’est une formule de correction .

Ne cherchons pas à justifier a priori une méthode en utilisant un polynôme d’interpolation ou un autre et écrivons brutalement un schéma multi-pas sous la forme générale suivante.

On suppose que y ⁰, y ¹, ..., y ^q-1 sont obtenus par une méthode à un pas convergente; on écrit:

où les 見ⁱ et 廓ⁱ sont des constantes données, indépendantes de h , de p et de f .

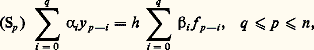Dans la suite, nous chercherons des valeurs des 見ⁱ et des 廓ⁱ pour que la méthode soit aussi efficace que possible. Nous supposerons que 見⁰ 0.

Pour p = q , on obtient:

Si 廓⁰ = 0, le système (S^q ) définit explicitemnt y ^q par une formule du type:

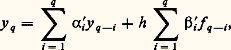puisque y ⁰, ..., y ^q-1 sont connus; de proche en proche, on obtient y ^q , y ^q+1 , ..., y ⁿ en calculant à chaque étape y ^q par une formule du type:

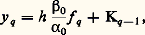où K^q-1 est connu. Si h est suffisamment petit, on démontre, comme précédemment, que l’équation précédente (en y ^q ) possède une solution unique qui peut être obtenue par itération; il suffit en effet que:

de proche en proche, on obtient y ^p , pour q 諒 p 諒 n , en résolvant chaque S^p .

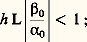On peut encore définir les notions de consistance (par rapport au problème posé) et de stabilité. Contentons-nous de donner certains résultats de convergence.

Nous dirons que la méthode précédente est convergente si:

tend vers 0 lorsque N augmente indéfiniment.

Cela suppose donc que les y ⁱ , pour 0 諒 i 諒 q 漣 1, ont été définis par une méthode à un pas convergente.

Considérons alors les polynômes: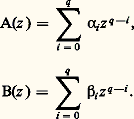

Ces polynômes A et B définissent la méthode multi-pas, puisque S^p est défini par les 見ⁱ et par les 廓ⁱ .

Une condition suffisante de convergence est donnée par le théorème suivant.

Théorème. Si A(1) = 0 et si A (1) = B(1), si de plus les racines z ⁱ de A satisfont à |z ⁱ | 諒 1, pour 1 諒 i 諒 q , et si les racines de module égal à 1 sont toutes simples, alors la méthode définie par les polynômes A et B est convergente.

On peut obtenir aussi des conditions pour que la méthode soit d’ordre k .

Encyclopédie Universelle. 2012.